문제
땅 위에 달팽이가 있다. 이 달팽이는 높이가 V미터인 나무 막대를 올라갈 것이다.
달팽이는 낮에 A미터 올라갈 수 있다. 하지만, 밤에 잠을 자는 동안 B미터 미끄러진다. 또, 정상에 올라간 후에는 미끄러지지 않는다.
달팽이가 나무 막대를 모두 올라가려면, 며칠이 걸리는지 구하는 프로그램을 작성하시오.
문제 해석
높이가 V 인 나무가 있고 낮에 A만큼 올라가고, 밤에 B만큼 내려간다. 단, 낮에 V에 도달하면 날짜를 세지 않고 종료한다.
예를 들어 높이가 5인 나무를 낮에 2, 밤에 1 이라고 할 때,
1일차 위치 : 1
2일차 위치 : 2
3일차 위치 : 3
4일차 낮의 위치 : 5
풀이
밤에는 거리가 감소하므로, 밤에는 목적지에 도착할 수가 없다.
낮에만 도착이 가능한데, 나무 V 를 하루 이동거리(A - B)로 나누어 버리게 되면, 마지막 날 도착을 했어도 B 만큼 빠져버리는 상황이 발생한다.
따라서, 도착하는 마지막 날 낮의 위치는 처음부터 없었다고 생각을 하고 나중에 날짜를 1번 더해주는 것으로 접근한다.
그럼 나무의 길이 V 는 V - A(낮 이동거리) 로 줄어든다.

하루에 이동하는 거리는 A - B (낮 이동거리 - 밤 이동거리) 이다.
만약에, 현재 나무의 길이(V - A) 를 하루 이동 거리(A - B) 로 나누었을 때,
정확히 나누어 떨어진다면, 몫은 걸린 날짜가 된다.
A = 2, B = 1, V = 5 라고 가정하자.

이 때의 걸린 날짜는 정확히 나누어 떨어지므로, 몫 3 이 정답이 된다.
처음에 낮에 1번을 이미 이동한 것 처럼 빼주었으므로, 3 + 1 하여 총 4일이 걸리게 된다.
만약에, 현재 나무의 길이(V - A) 를 하루 이동 거리(A - B) 로 나누었을 때,
위처럼 나누어 떨어지지 않을 경우도 생각해야한다.
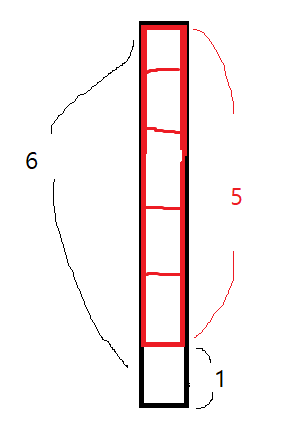
A = 5, B = 1, V = 6 이라고 가정하자.
몫은 0 이 나오게 되고 나누어 떨어지지 않는다.
이 말은, 몫 만큼 날짜가 걸리고도 아직 거리가 앞으로 무조건 1번 이동할 만큼 남았다는 뜻이 된다.
따라서, 몫 + 1(남은 거리만큼 하루) + 1(처음 뺀 이동거리) 만큼 날짜가 걸리게 된다.
정리하면, 몫 + 2가 정답이 된다.
구현
#include <iostream>
using namespace std;
int main()
{
int day; int night; int tree; // 낮, 밤, 나무
cin >> day >> night >> tree;
if ((tree - day) % (day - night) == 0) // 나누어 떨어진다면
{
cout << (tree - day) / (day - night) + 1;
}
else cout << (tree - day) / (day - night) + 2; // 나머지가 생기면
}'백준 알고리즘 단계별 풀이 (문제 수) > 기본 수학 1 (8)' 카테고리의 다른 글
| [C++] 부녀회장이 될테야 : 2775번 (0) | 2022.07.04 |
|---|---|
| [C++] ACM 호텔 : 10250번 (0) | 2022.07.04 |
| [C++] 분수 찾기 : 1193번 (0) | 2022.07.04 |
| [C++] 벌집 : 2292번 (0) | 2022.07.04 |
| [C++] 손익분기점 : 1712번 (0) | 2022.07.03 |


